线性表

线性表的基础概念

定义

n(n >= 0)个具有相同特性数据元素的有限序列

基本特性

有且仅有一个第一个元素，有且仅有一个最后元素。
出第一元素外，其他元素都有唯一的直接前趋。
除最后元素外，其他元素都有唯一的直接后继。

常见运算

初始化线性表
表置空
求线性表中第 i 个元素
查找满足条件的数据元素
插入
删除
查找某个元素前趋/后继
排序

ADT

基础概念

是一种抽象数据类型，包含
- 对数据的定义
- 对关系的定义
- 对运算的定义
‘{D, S, P}’
- D：数据集合
- S：关系集合
- P：操作的集合
通过固有数据类型实现

线性表的例子

ADT	triplet
数据对象	D = ‘{v1, v2, v3}’
数据关系	R = ‘{<v1, v2>, <v2, v3>}’
基本操作
init_triplet(&T, n1, n2, n3)	结果：构造三元组 T，对元素 v1,v2,v3 分别赋以 n1,n2,n3 的值
max(T, &e)	条件：存在；结果：找到 T 中数据元素的最大值，用 e 返回\

顺序存储及运算

定义

在内存中开辟连续的存储空间，用连续的存储单元依次存放线性表的元素。

cpp

#define MAXSIZE maxlen
typedef int ele;
typedef struct{
    ele v[MAXSIZE];
    int len;
}sqlist;

特点

逻辑上相邻的数据元素，其物理位置也相邻。
利用物理位置上的关系，反映元素的逻辑关系。
扩展不灵活，容易造成空间浪费。
顺序表是一种随机存取的存储结构。
静态操作容易实现。
动态操作实现效率低。

基础操作

初始化，构建空顺序表。
求表长
查找：查找成功时的 ASL = (n+1)/2
插入
- 将从最后一个元素到位置 i 的每个元素依次向后移动*（主要时间消耗）*一个位置。
- 将 x 写到第 i 个位置上。
- ASL = n/2
删除：实际操作为依次向前赋值，ASL = (n-1)/2

删除重复元素

已知顺序表的元素按非降序排列。请编写算法，删除表中的重复元素。例如，原表为（1，1，2，3，3，3，4，5，5），经算法处理后，表为（1，2，3，4，5）。要求算法的空间复杂度为 O(1)，不需输出表元素的值。

cpp

#include<iostream>
using namespace std;

int const MAXLEN = 100;

typedef struct t{
    int data[MAXLEN];
    int len;
}LIST;

void del(LIST* list, int index){
    for(int k = index+1; k < list->len; index++, k++){
        list->data[index] = list->data[k];
    }
    list->len--;
}

void PackList(LIST* list){
    for(int i = 0; i < list->len; i++){
        for(int j = i + 1; j < list->len; j++){
            if(list->data[i] == list->data[j]){
                del(list, j);
                j--;
            }
        }
    }
}

void print_list(LIST* list){
    cout << "[";
    for(int i = 0; i < list->len; i++){
        cout << list->data[i] << ", ";
    }
    cout << "]" << endl;
}

int main(){
    LIST list ={{1, 1, 2, 3, 3, 3, 4, 5, 5}, 9};
    print_list(&list);
    PackList(&list);
    print_list(&list);
    return 0;
}
/*输出：
[1, 1, 2, 3, 3, 3, 4, 5, 5, ]
[1, 2, 3, 4, 5, ]
*/

链式存储及运算

基础概念

基本特性：用一组物理位置任意的存储单元存储线性表的结点，物理位置的关系不能反映结点间的逻辑关系。
结构：数据域=>存储元素本身的信息；指针域=>结点的直接后继结点的内存地址。

cpp

typedef char ele;
struct node{
    ele data;
    struct node *node;
}

头结点：辅助结点，后面做增删改查的时候头节点是不变的，函数也可以不需要返回值就行。

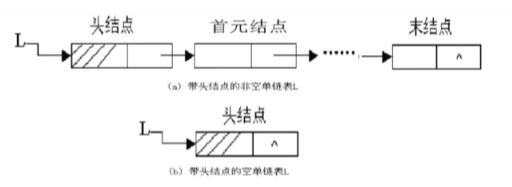
注：创建结点时需要开辟内存，删除结点时记得释放空间。

基础操作

定义结构

cpp

#include<iostream>
#include<exception>
#include<stdexcept>

using namespace std;
struct ListNode {
	int key;
	struct ListNode *next;
	ListNode(int x) :
			key(x), next(NULL) {
	}
};

创建带头结点的单链表(尾插与头插)

cpp

void init_list(ListNode* head, bool head_or_tail = true){
    ListNode* temp = NULL;
    if(head_or_tail == true){
        for(int i = 0; i < 4; i++){
            temp = new ListNode(i);
            temp->next = head->next;
            head->next = temp; 
        }
    }else{
        ListNode* tail = head;
        for(int i = 0; i < 4; i++){
            temp = new ListNode(i);
            tail->next = temp;
            tail = tail->next;
        }
    }
}

取表中第 i 个元素的键值

cpp

int get_value(ListNode* head, int index){
    //首元节点为第一个节点，即 index 从 1 开始
    if(index <= 0){
        throw std::out_of_range( "negative number!" );
    }
    int i = 0;
    ListNode* p = head;
    while(i < index && p->next != NULL){
        p = p->next;
        i++;
    }
    if(i > index){
        throw std::out_of_range("index out of the range!");
    }
    return p->key;
}

删除表中的某个结点

cpp

void del_node(ListNode* head, int index){
    //首元节点为第一个节点，即 index 从 1 开始
    if(index <= 0){
        throw std::out_of_range( "negative number!" );
    }
    int i = 1;
    ListNode* p = head->next;
    ListNode* pre = NULL;
    for(;p->next != NULL; i++){//使 p 指向要删除的节点
        if(i == index){
            break;
        }
        pre = p;
        p = p ->next;
    }
    if(i < index){
        throw std::out_of_range( "index out of the range!" );
    }
    pre->next = p->next;//del
    p->next = NULL;
}

向表中插入某个结点

cpp

void insert(ListNode* head, int pos, int key){
    //0 代表的就是从头部添加，1 代表的就是在首元节点后添加；
    if(pos < 0){
        throw std::out_of_range( "negative number!" );
    }
    ListNode* t = new ListNode(key);
    ListNode* p = head;//寻找要添加的位置的前一个节点
    int i = 0;
    for(;p->next != NULL; i++){
        if(i == pos){
            break;
        }
        p = p->next;
    }
    if(i < pos){
        throw std::out_of_range( "index out of the range!" );
    }
    t->next = p->next;
    p->next = t;
}

搜索结点

cpp

int search(ListNode* head, int key){
    //-1 代表没找到，找到返回对应的第一次下标
    ListNode* p = head->next;
    int i = 1;
    for(; p-> next != NULL; i++){
        if(p->key == key){
            return i;
        }
        p = p->next;
    }
    if(p->key == key){//尾节点还没判断
        return i+1;
    }
    return -1;
}

主函数

cpp

int main(){
    //头插法
    ListNode* head1 = new ListNode(-1);
    init_list(head1);
    print_list(head1);//[3, 2, 1, 0]
    //尾插法
    ListNode* head2 = new ListNode(-1);
    init_list(head2, false);
    print_list(head2);//[0, 1, 2, 3]
    //获取值
    cout << get_value(head1, 1) << endl;//3
    //删除节点
    del_node(head1, 2);
    print_list(head1);//[3, 1, 0]
    //在头尾以及任意位置插入节点
    insert(head2, 3, 10);
    print_list(head2);//[0, 1, 2, 10, 3]
    insert(head2, 0, 10);
    print_list(head2);//[10, 0, 1, 2, 10, 3]
    int a = search(head2, 2);
    int b = search(head2, 9);
    cout << a << "," << b << endl;//4,-1
    return 0;
}

循环链表

链表最后一个结点的指针域不是 null，而是头结点的地址，表形成一个环。

双向链表

分别指向直接前趋和直接后继：

cpp

typedef struct dulnode{
    ele data;
    struct dulnode *next, prior;
}

对称性：前趋的后继就是它自己。

在双向链表结点 P 之前插入 S 结点：

cpp

s->prior = p->prior;
p->prior->next = s;
s->next = p;
p->prior = s;

删除结点：

cpp

p->prior->next = p->next;
p->next->prior = p->prior;
delete(p);//释放空间

总结对比

从时间角度
- 按位置查找元素、或查找元素的前趋和后继，顺序存储有较大优势。
- 插入数据、删除数据，链式存储有较大优势。
从空间角度
- 顺序表的存储空间是静态分配的，在程序执行前必须规定其存储规模。
- 链表的存储空间是动态分配的，只要内存空间有空闲，就不会溢出。

	顺序存储	链式存储
循环变量	下标变量 i	指针变量 p
初始化	i = 0	head=null 或 head->next=null
处理对象	a[j], *(a+i)	*p
下一对象	i = i + 1	p = p->next
循环条件	i < len	p != null

基础经典题型

编写函数，从一个顺序表 A 中删除元素值在 x 和 y(x≤y)之间的所有元素

cpp

#include<iostream>
#include<stdexcept>
using namespace std;

int const MAXLEN = 100;

typedef struct t{
    int data[MAXLEN];
    int len;
}LIST;

void del_one(LIST * nums, int index){
    int j = index + 1;
    for(;j < nums->len; index++, j++){
        nums->data[index] = nums->data[j];
    }
    nums->len--;
}

void del_range(LIST * nums, int x, int y){
    if(x > y){
        throw std::out_of_range( "invalid parameter:x > y" );
    }
    for(int i = 0; i < nums->len; i++){
        if(nums->data[i] >= x && nums->data[i] <= y){
            del_one(nums, i);
            i--;
        }
    }
}

void print_list(LIST* list){
    cout << "[";
    for(int i = 0; i < list->len; i++){
        cout << list->data[i] << ", ";
    }
    cout << "]" << endl;
}

int main(){
    //初始化顺序表
    LIST nums = {{1, 2, 3, 4, 5, 6, 7, 8}, 8};
    print_list(&nums);
    del_range(&nums, 4, 7);
    print_list(&nums);
    /*
    [1, 2, 3, 4, 5, 6, 7, 8, ]
    [1, 2, 3, 8, ]  
    */
    return 0;
}

编写函数，将一个顺序表 A（有 n 个元素且任何元素均不为 0），分拆成两个顺序表 B 和 C。使 A 中大于 0 的元素存放在 B 中，小于 0 的元素存放在 C 中，返回顺序表 B 和 C。

cpp

#include<iostream>
#include<vector>
using namespace std;

int const MAXLEN = 100;

typedef struct t{
    int data[MAXLEN];
    int len;
}LIST;

vector<LIST*> ab;

void cut_list(LIST* nums){
    LIST a1;
    LIST b1;
    LIST * a = &a1;
    LIST * b = &b1;
    a->len = 0;
    b->len = 0;
    for(int i = 0, j = 0, k = 0; i < nums->len; i++){
        if(nums->data[i] > 0){
            a->data[j] = nums->data[i];
            j++;
            a->len++;
        }else{
            b->data[k] = nums->data[i];
            k++;
            b->len++;
        }
    }
    ab.push_back(a);
    ab.push_back(b);//这里这样操作是为了返回两个值
}

int main(){
    LIST nums = {{-1, -2, -3, -4, 5, 6, 7, 8}, 8}; 
    LIST *a,  *b;
    cut_list(&nums);
    a = ab[0];
    b = ab[1];
    return 0;
}

已知一个单链表，编写一个函数将该单链表复制到另一个单链表中。

cpp

ListNode * list_copy(ListNode* head){
    if(head->next == NULL){
        throw std::out_of_range( "empty list!" );
    }
    ListNode* c_head = new ListNode(-1);
    ListNode* tail = c_head;//尾插法辅助变量
    ListNode* p = head->next;
    ListNode* c_p = NULL;
    while(p->next != NULL){
        c_p = new ListNode(p->key);
        tail->next = c_p;
        tail = tail->next;
        p = p->next;
    }
    c_p = new ListNode(p->key);
    tail->next = c_p;
    return c_head;
}

int main(){
    ListNode* head1 = new ListNode(-1);
    init_list(head1);
    ListNode* head2 = list_copy(head1);
    print_list(head2);
    head2->next->key = 5;
    print_list(head1);
    print_list(head2);    
    /*
    [3, 2, 1, 0]
    [3, 2, 1, 0]
    [5, 2, 1, 0]
    */
    return 0;
}

如下类型定义：
typedef struct node
’{ int exp; //指数
float coef; //系数
struct node *next;
}‘polynode;
【要求】用链式存储结构实现：生成两个多项式 PA 和 PB，求 PA 和 PB 之和，并输出“和多项式”。

cpp

#include<iostream>
using namespace std;

struct polynode {    
    int exp;       //指数
    float coef;     //系数
    struct polynode *next;
    polynode(int x, float y) :
        exp(x),coef(y),next(NULL) {
	}
};

void init1(polynode* head){
    polynode* p = head;
    polynode* temp;
    for(int i = 0; i < 5; i++){
        temp = new polynode(i, i);
        temp->next = p->next;
        p->next = temp;
    }
}

void init2(polynode* head){
    polynode* p = head;
    polynode* temp;
    for(int i = 1; i < 6; i++){
        temp = new polynode(i, i);
        temp->next = p->next;
        p->next = temp;
    }
}

void combine(polynode* head1, polynode* head2){
    if(head1->next == NULL || head2->next == NULL)return;
    //head2 为合成后的链
    polynode* p1 = head1->next;
    polynode* p2 = head2->next;
    //类似于冒泡排序找相同底的数，找到就合在一起，否则就多增加一个节点
    int flag = 0;
    while(p1->next != NULL){
        p2 = head2->next;
        //因为后面增加了一个节点的话，就需要从头开始遍历
        while(p2->next != NULL){
            if(p1->coef == p2->coef){
                p2->exp = p1->exp + p2->exp;
                flag = 1;
            }
            p2 = p2->next;
        }
        if(p1->coef == p2->coef){//p2 还剩一个尾节点
            p2->exp = p1->exp + p2->exp;
            flag = 1;
        }
        if(flag == 0){//把 p1 插进去
            p1->next = head2->next;
            head2->next = p1;
        }
        flag = 0;
        p1 = p1->next;
    }


    while(p2->next != NULL){//p1 还剩一个尾节点
        if(p1->coef == p2->coef){
            p2->exp = p1->exp + p2->exp;
            flag = 1;
        }
        p2 = p2->next;
    }
    if(p1->coef == p2->coef){//还剩一个尾节点
        p2->exp = p1->exp + p2->exp;
        flag = 1;
    }
    if(flag == 0){//把 p1 插进去
        p1->next = head2->next;
        head2->next = p1;
    }
    p1 = p1->next;
}

void print_list(polynode* head){//改一下
    if(head->next == NULL){
        cout << "[]" << endl;
        return;
    }
    cout << "[";
    polynode* p = head->next;
    while(p->next != NULL){
        cout << p->coef <<  "^"<< p->exp << ", ";
        p = p->next;
    }
    cout << p->coef <<  "^"<< p->exp;
    cout << "]" << endl;
}


int main(){
    polynode* head1 = new polynode(-1, -1);
    polynode* head2 = new polynode(-1, -1);
    init1(head1);
    print_list(head1);
    init2(head2);
    print_list(head2);
    combine(head1, head2);
    print_list(head2);
/*输出
[4^4, 3^3, 2^2, 1^1, 0^0]
[5^5, 4^4, 3^3, 2^2, 1^1]
[0^0, 5^5, 4^8, 3^6, 2^4, 1^2]
*/
    return 0;
}

约瑟夫生者死者问题。据说著名犹太历史学家 Josephus 有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与 Josephus 及他的朋友躲到一个洞中，39 个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式：41 个人排成一个圆圈，由第 1 个人开始报数，每报数到第 3 人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而 Josephus 和他的朋友并不想遵从，Josephus 要他的朋友先假装遵从，他将朋友与自己安排在第 16 个与第 31 个位置，于是逃过了这场死亡游戏。这就是著名的约瑟夫生者死者问题。
17 世纪的法国数学家加斯帕在《数目的游戏问题》中也讲了这样一个故事：15 个教徒和 15 个非教徒在深海上遇险，必须将一半的人投入海中，其余的人才能幸免于难，于是想了一个办法：30 个人围成一圆圈，从第一个人开始依次报数，每数到第九个人就将他扔入大海，如此循环进行直到仅余 15 个人为止。【问题】怎样的安排才能使每次投入大海的都是非教徒？
请编程解决这一 n(1≤n≤30)个人的跳海问题。要求分别用两种线性表的存储结构来解决。【提示】在使用链式存储结构时，可构造具有 30 个结点的单循环链表。

cpp

#include<iostream>
#include<cstring>
using namespace std;

void solution1(){
    int nums[30];
    memset(nums,0,sizeof(nums));
    //C++内置方法初始化数组全部为 0
    //循环 15 次，找出会死的位置；
    for(int i = 0,count = 0; count < 15*9; i++,count++){
        if(i >= 30){
            i = i - 30;
        }
        if(nums[i] == 1){
            i++;//跳过死人
        }
        if(count%9 == 0){//标记死人
            nums[i] = 1;
        }
    }
    cout << "[";
    for(int i = 0; i < 30; i++){
        cout << nums[i] << ", ";
    }
    cout << ']' << endl;
}

struct listnode{
    int dead;
    int index;
    listnode* next;
    listnode(int x):
        dead(0),index(x),next(NULL){}
};

void solution2(){
    //创建一个 30 个节点的循环列表;
    listnode* p = NULL;
    listnode* p1 = new listnode(0);//首元节点
    listnode* tail = p1;
    for(int i = 1; i < 30; i++){
        p = new listnode(i);
        tail->next = p;
        tail = tail->next;
    }
    tail->next = p1;//头尾相连
    //开始死人
    p = p1;
    for(int count = 0; count < 15*9; count++){
        if(p->dead == 1){
            p = p->next;//跳过死人
        }
        if(count%9 == 0){//标记死人
            p->dead = 1;
        }
        p = p->next;
    }
    //输出要死的位置
    p = p1;
    cout << "[";
    for(int i = 0; i < 30; i++){
        cout << p->dead << ", ";
        p = p->next;
    }
    cout << "]" << endl;
}

int main(){
    cout << "solution1:" << endl;
    solution1();
//[1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 
//0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, ]
    cout << "solution2:" << endl;
    solution2();
//结果一致，相比于上面一种，仅仅在计数值超过 30 时不需要重置计数值
//因为是循环链表，其他的思路也都是一致的
    return 0;
}

线性表 ​

线性表的基础概念 ​

定义 ​

基本特性 ​

常见运算 ​

ADT ​

基础概念 ​

线性表的例子 ​

顺序存储及运算 ​

定义 ​

特点 ​

基础操作 ​

链式存储及运算 ​

基础概念 ​

基础操作 ​

定义结构 ​

创建带头结点的单链表(尾插与头插) ​

取表中第 i 个元素的键值 ​

删除表中的某个结点 ​

向表中插入某个结点 ​

搜索结点 ​

主函数 ​

循环链表 ​

双向链表 ​

总结对比 ​

基础经典题型 ​

线性表

线性表的基础概念

定义

基本特性

常见运算

ADT

基础概念

线性表的例子

顺序存储及运算

定义

特点

基础操作

链式存储及运算

基础概念

基础操作

定义结构

创建带头结点的单链表(尾插与头插)

取表中第 i 个元素的键值

删除表中的某个结点

向表中插入某个结点

搜索结点

主函数

循环链表

双向链表

总结对比

基础经典题型