回溯与分支极限

回溯

关于回溯

• 许多问题很难用算法求解，但是又不得不解决；
• 回溯搜索问题的解空间，可以看作穷举查找的改进，可解决规模较大的组合难题；
• 回溯通常按照深度优先、宽度优先或者结合的方式等多种方法遍历树；

n 皇后问题

TODO

哈密顿回路

TODO

子集和问题

TODO

分支界限

概述

在此之前，你应该知道回溯的方法

和回溯法相比，分支界限法需要两个额外的条件：

• 对于一颗状态空间树的每一个节点所代表的部分解，我们提供一种方法，计算出通过这个部分解繁衍出的任何解在目标函数上的最佳边界。
• 目前求得的最佳解的值。

在最小化问题中不小于，在最大化问题中不大于目前的最佳解，这个节点就是一个没有希望的节点，需要立即终止（剪枝）

一般来说，只要符合下面三种中的一种原因，我们就会终止它在当前节点上的查找路径：

• 该节点的边界值不能超越目前最佳解的值。
• 该节点无法代表任何可行解，因为它已经违反了问题的约束。
• 该节点代表的可行解的子集只包含一个单独的点（因此无法给出更多的选择）。在这种情况下，我们拿这个可行解在目标函数上的值和目前求得的最佳解进行比较，如果新的解更好一些，就用前者替换后者。

分支界限求旅行商问题(图示)

问题：寻找最小成本分配

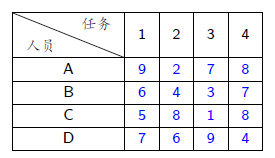
成本下界：任何解的成本不会小于每行最小元素之和，即 2+3+1+4=10；

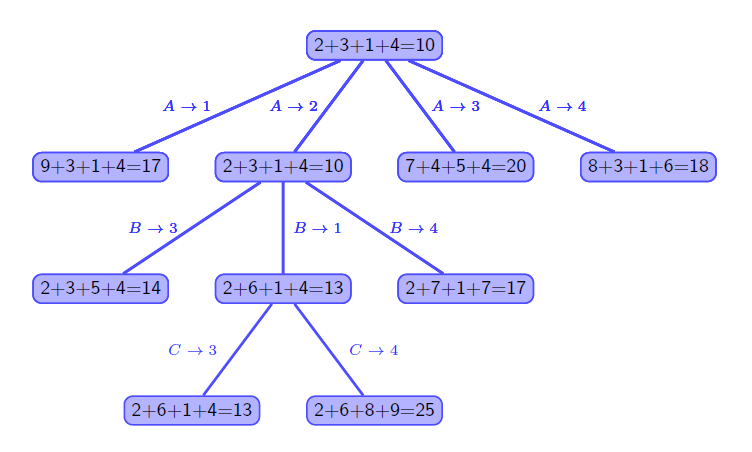
分支界限求背包问题(图示)

问题：装入承重量 W=10 的背包价值最大的物品

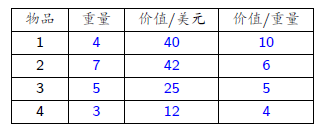
• 价值上界：对于给定实例中的物品，按照降序对”价值/重量“比排序；

• 依次装入还未装入背包价值最大的物品；

• 若已经选的物品总价值为$v$，重量为$w$，后续装入物品后总结之的上界$ub=\mathrm{背}\mathrm{包}\mathrm{剩}\mathrm{余}\mathrm{重}\mathrm{量}(W-w)\ast \mathrm{剩}\mathrm{下}\mathrm{物}\mathrm{品}\mathrm{最}\mathrm{佳}\mathrm{单}\mathrm{位}\mathrm{价}\mathrm{值}{v}_{i+1}/w_{i+1}$；

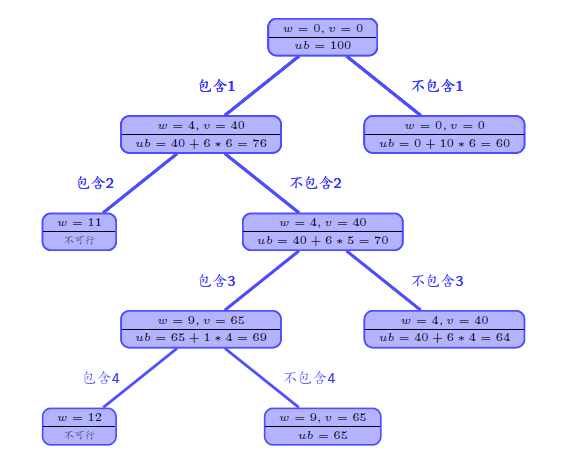
分支界限解决旅行商问题(代码)

import math

maxsize = float('inf')


def copyToFinal(curr_path):
    final_path[:N + 1] = curr_path[:]
    final_path[N] = curr_path[0]


def firstMin(adj, i):
    min = maxsize
    for k in range(N):
        if adj[i][k] < min and i != k:
            min = adj[i][k]

    return min


def secondMin(adj, i):
    first, second = maxsize, maxsize
    for j in range(N):
        if i == j:
            continue
        if adj[i][j] <= first:
            second = first
            first = adj[i][j]

        elif (adj[i][j] <= second and adj[i][j] != first):
            second = adj[i][j]

    return second

def TSPRec(adj, curr_bound, curr_weight, level, curr_path, visited):
    global final_res

    if level == N:

        if adj[curr_path[level - 1]][curr_path[0]] != 0:

            curr_res = curr_weight + adj[curr_path[level - 1]][curr_path[0]]
            if curr_res < final_res:
                copyToFinal(curr_path)
                final_res = curr_res
        return

    for i in range(N):

        if (adj[curr_path[level - 1]][i] != 0 and visited[i] == False):
            temp = curr_bound
            curr_weight += adj[curr_path[level - 1]][i]

            if level == 1:
                curr_bound -= (
                    (firstMin(adj, curr_path[level - 1]) + firstMin(adj, i)) /
                    2)
            else:
                curr_bound -= (
                    (secondMin(adj, curr_path[level - 1]) + firstMin(adj, i)) /
                    2)

            if curr_bound + curr_weight < final_res:
                curr_path[level] = i
                visited[i] = True

                TSPRec(adj, curr_bound, curr_weight, level + 1, curr_path,
                       visited)

            curr_weight -= adj[curr_path[level - 1]][i]
            curr_bound = temp

            visited = [False] * len(visited)
            for j in range(level):
                if curr_path[j] != -1:
                    visited[curr_path[j]] = True


def TSP(adj):

    curr_bound = 0
    curr_path = [-1] * (N + 1)
    visited = [False] * N

    for i in range(N):
        curr_bound += (firstMin(adj, i) + secondMin(adj, i))

    curr_bound = math.ceil(curr_bound / 2)

    visited[0] = True
    curr_path[0] = 0

    TSPRec(adj, curr_bound, 0, 1, curr_path, visited)

adj1 = [
    [0, 3, 1, 5, 8],
    [3, 0, 6, 7, 9],
    [1, 6, 0, 4, 3],
    [5, 7, 4, 0, 3],
    [8, 9, 2, 3, 0]
]
N = 5

final_path = [None] * (N + 1)

visited = [False] * N

final_res = maxsize

TSP(adj1)

print("Minimum cost :", final_res)
print("Path Taken : ", end=' ')
for i in range(N + 1):
    print(final_path[i], end=' ')

Minimum cost : 16
Path Taken :  0 1 3 4 2 0